Граф Рисунок (45 Фото)
Поделиться:
Поделиться:
Поделиться:
Поделиться:
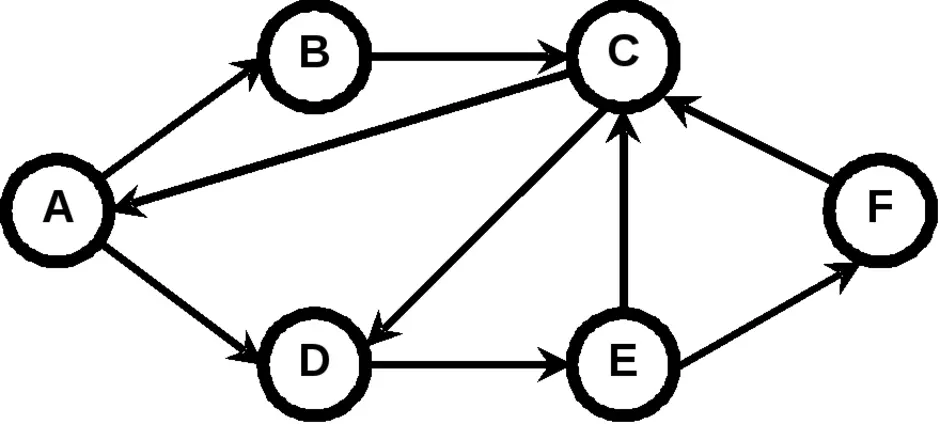
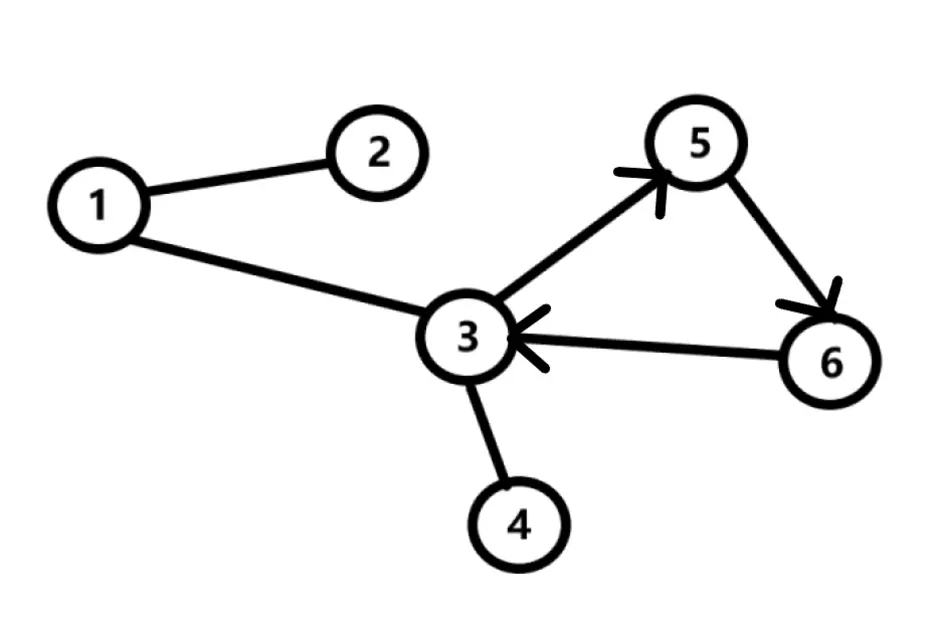
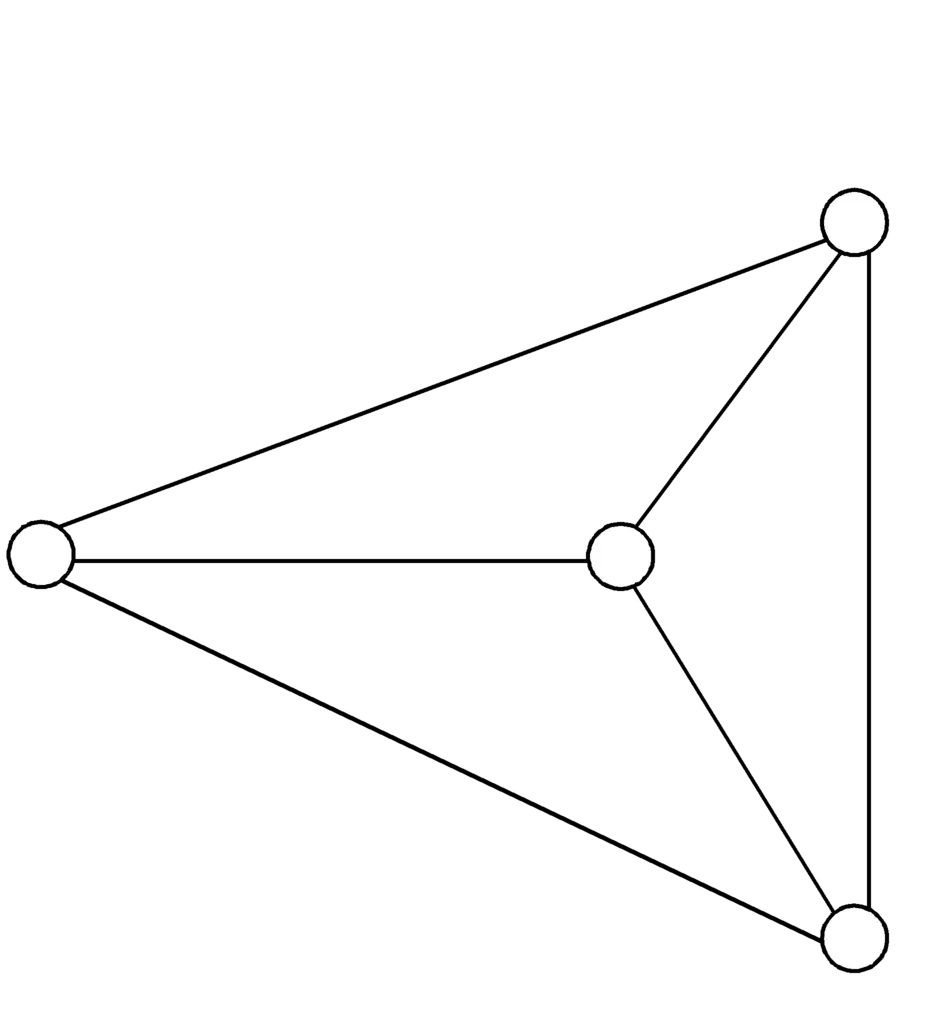
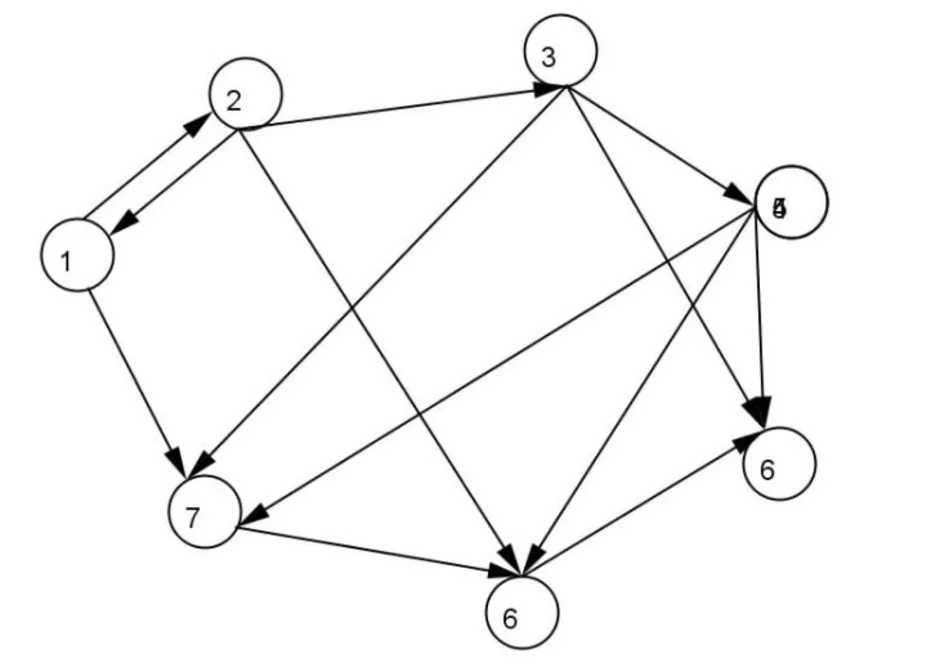
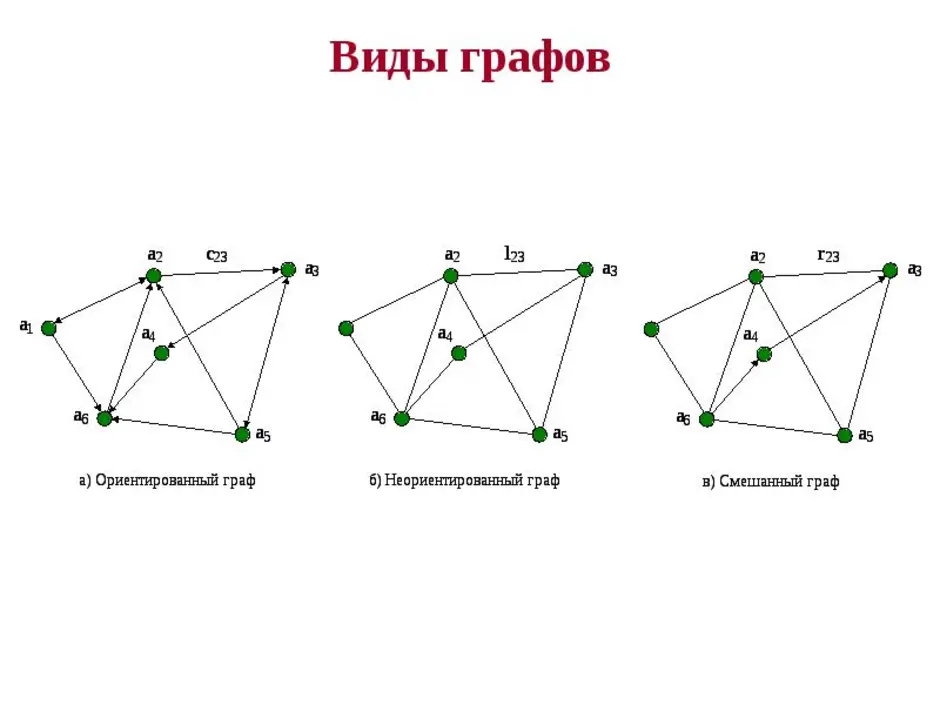
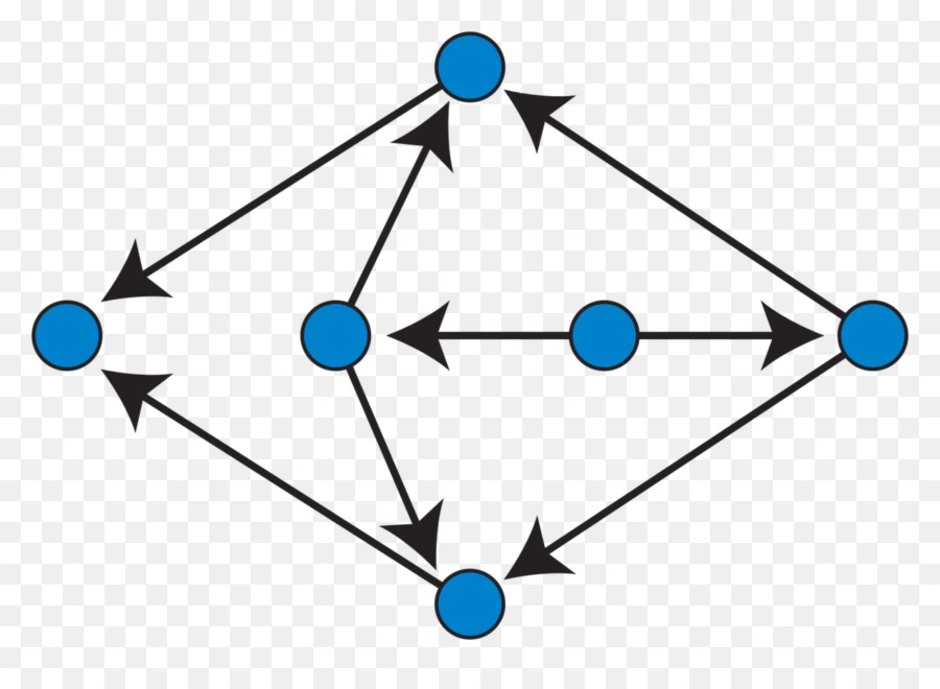
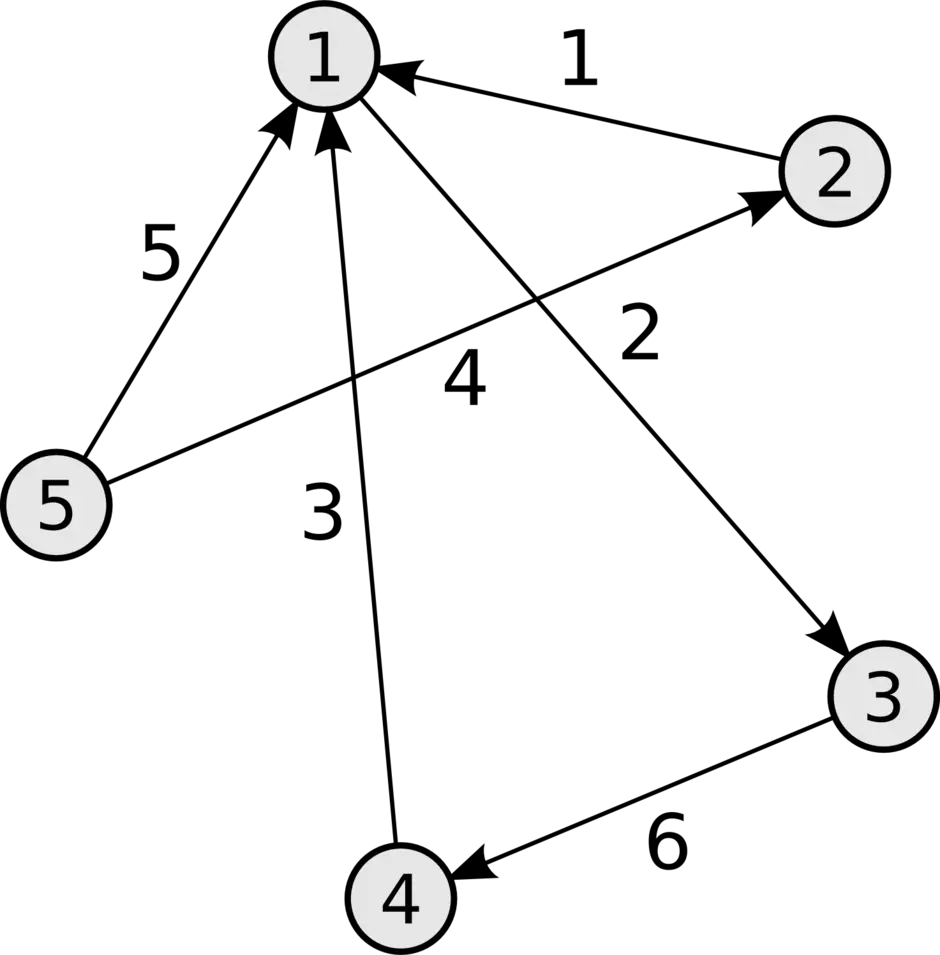
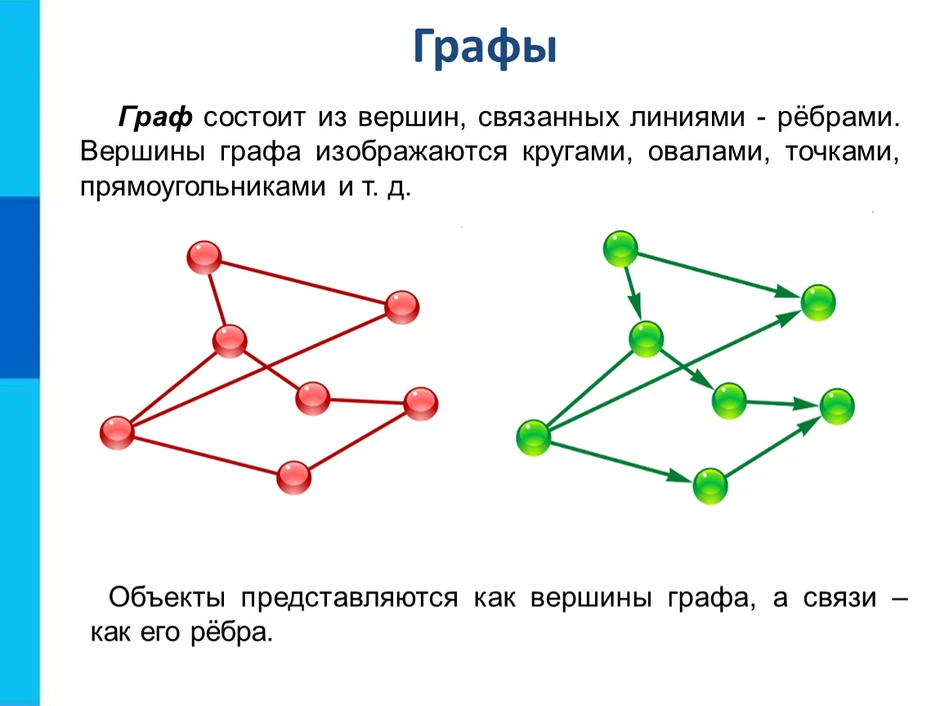
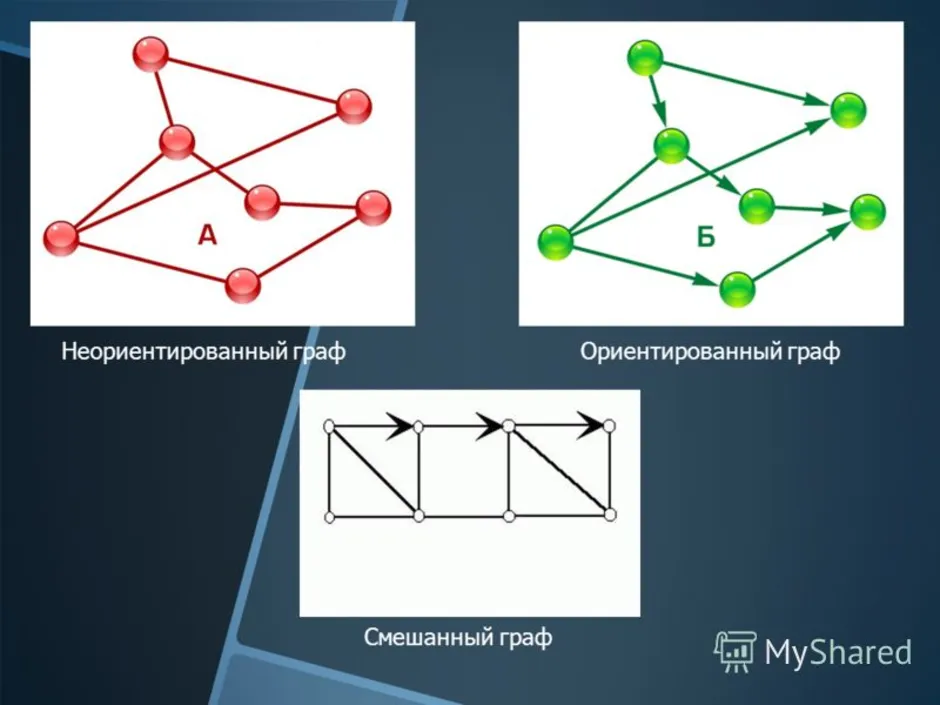
Граф, рёбрам которого присвоено направление. Направленные рёбра именуются также дугами, а в некоторых источниках и просто рёбрами. Граф, ни одному ребру которого не присвоено направление, называется неориентированным графом или неорграфом.
Поделиться:

Поделиться:
Поделиться:
Поделиться:
Поделиться:
Поделиться:
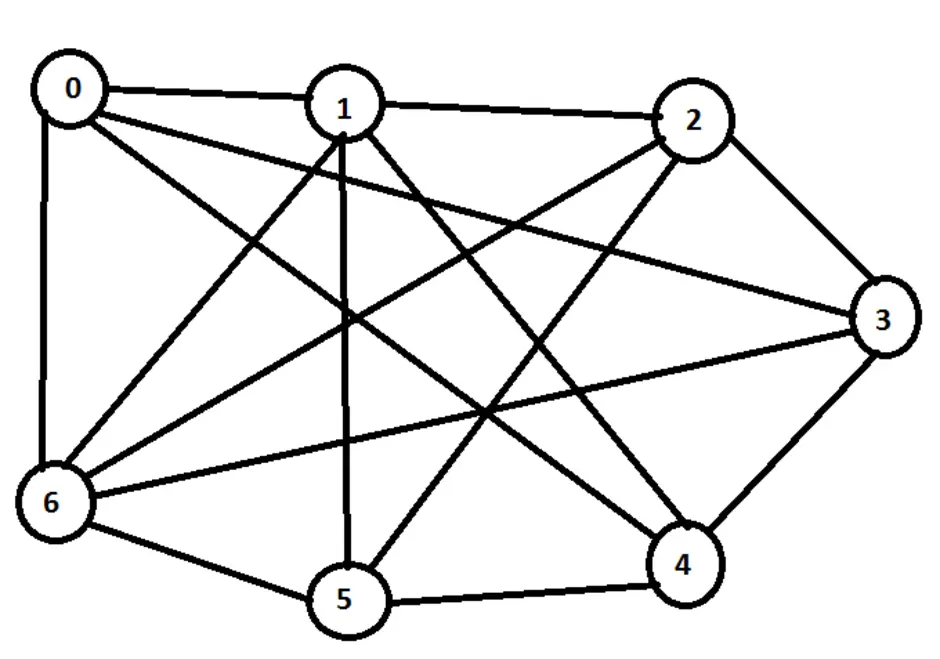
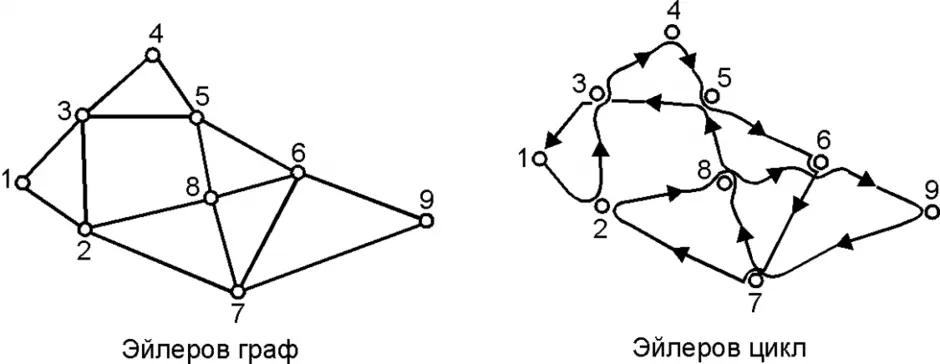
Это путь, проходящий по всем рёбрам графа и притом только по одному разу. Эйлеров цикл - эйлеров путь, являющийся циклом, то есть замкнутый путь, проходящий через каждое ребро графа ровно по одному разу.
Поделиться:
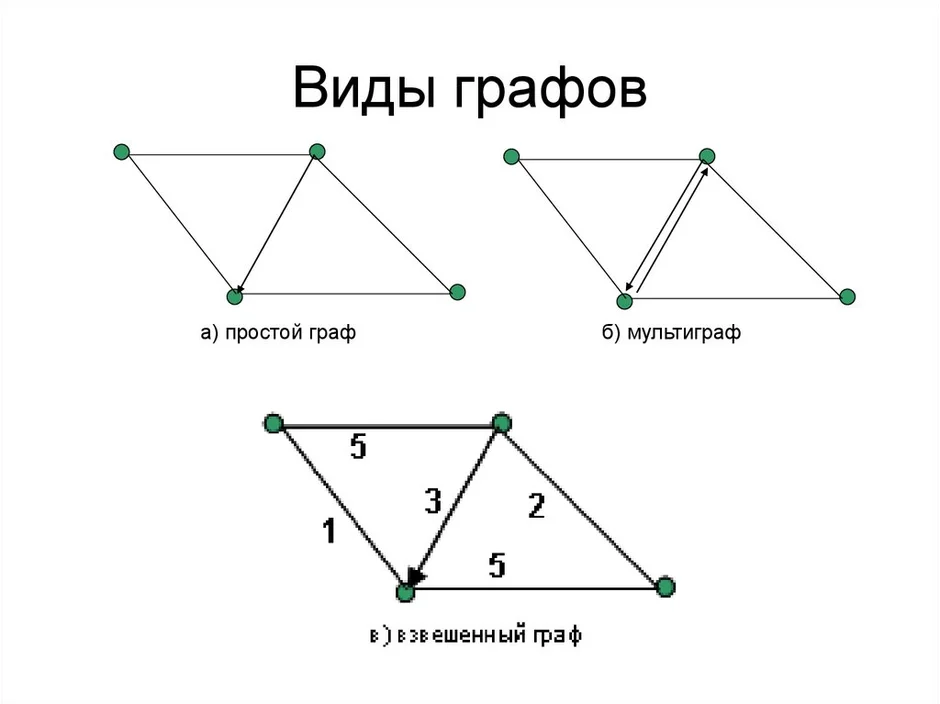
Поделиться:
Поделиться:
Поделиться:
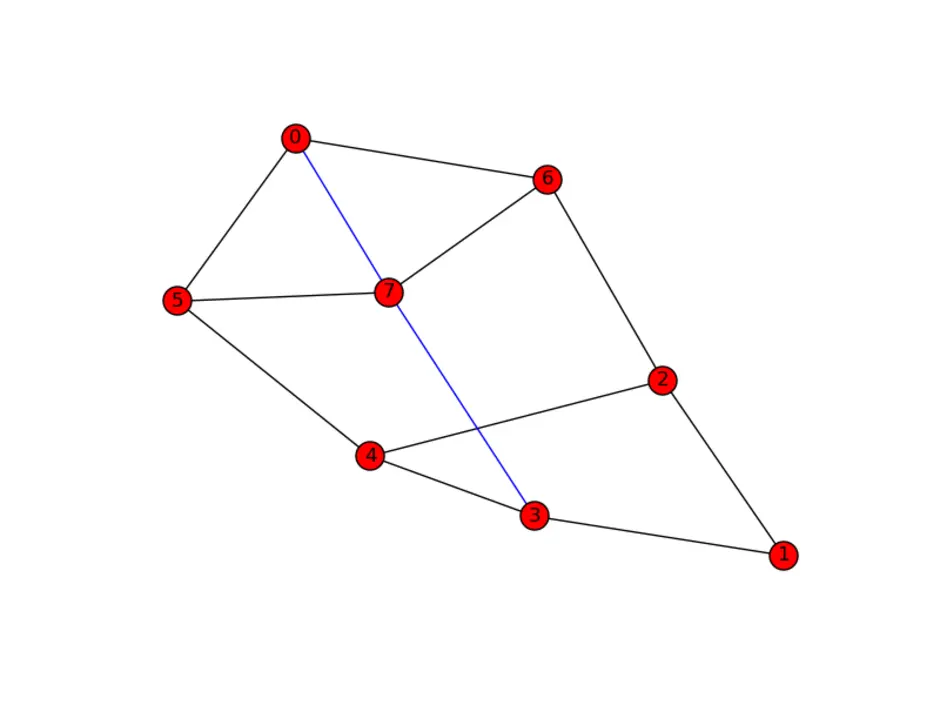
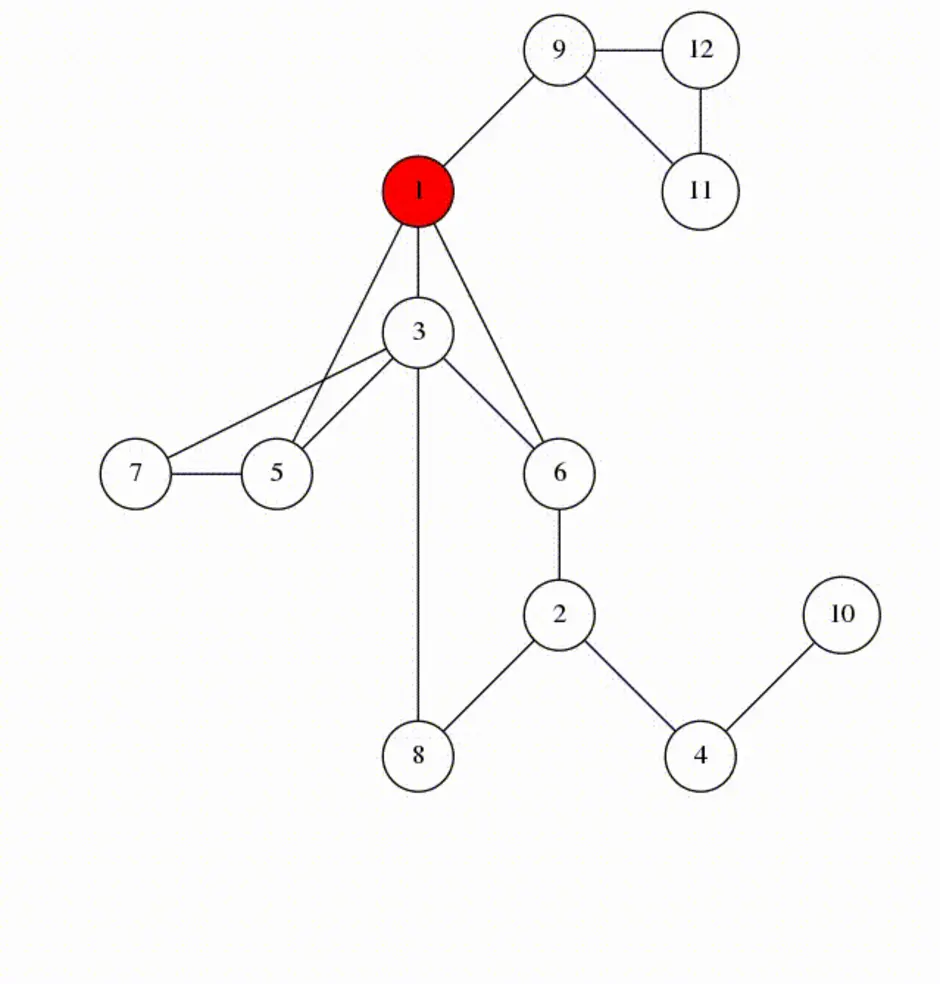
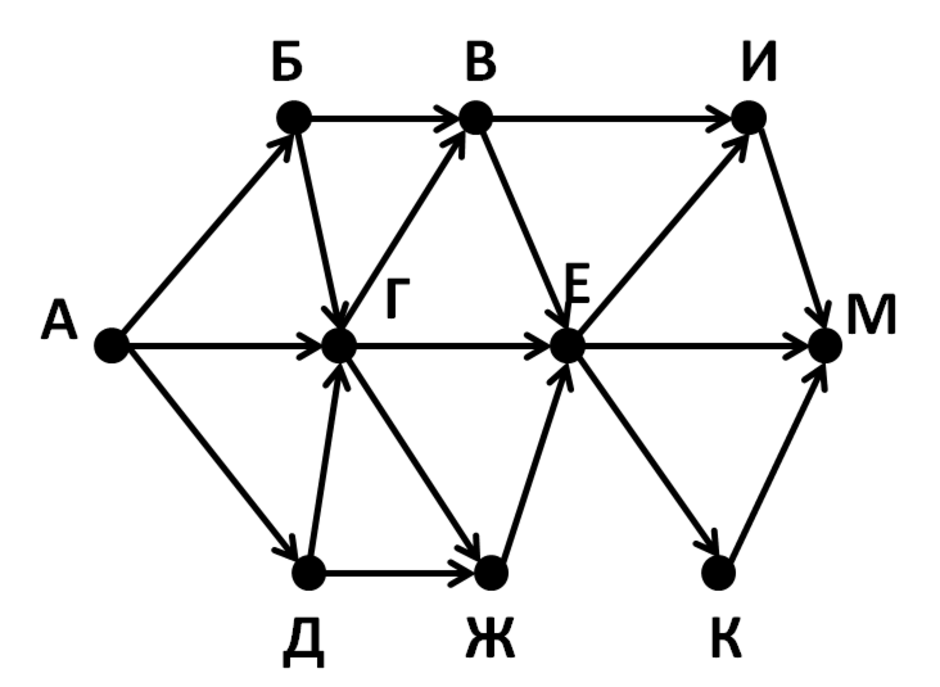
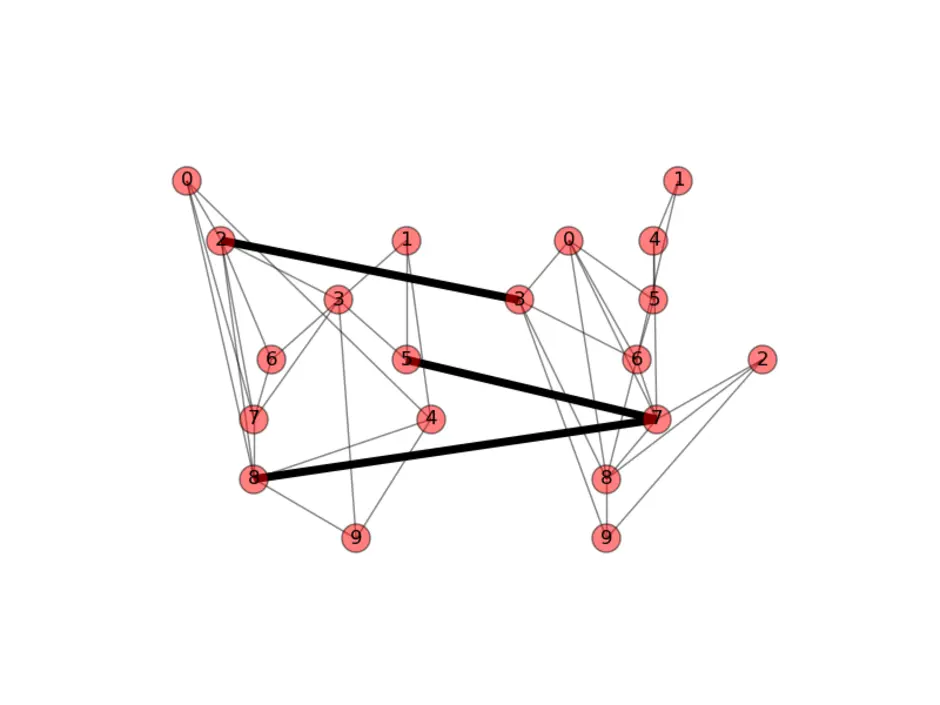
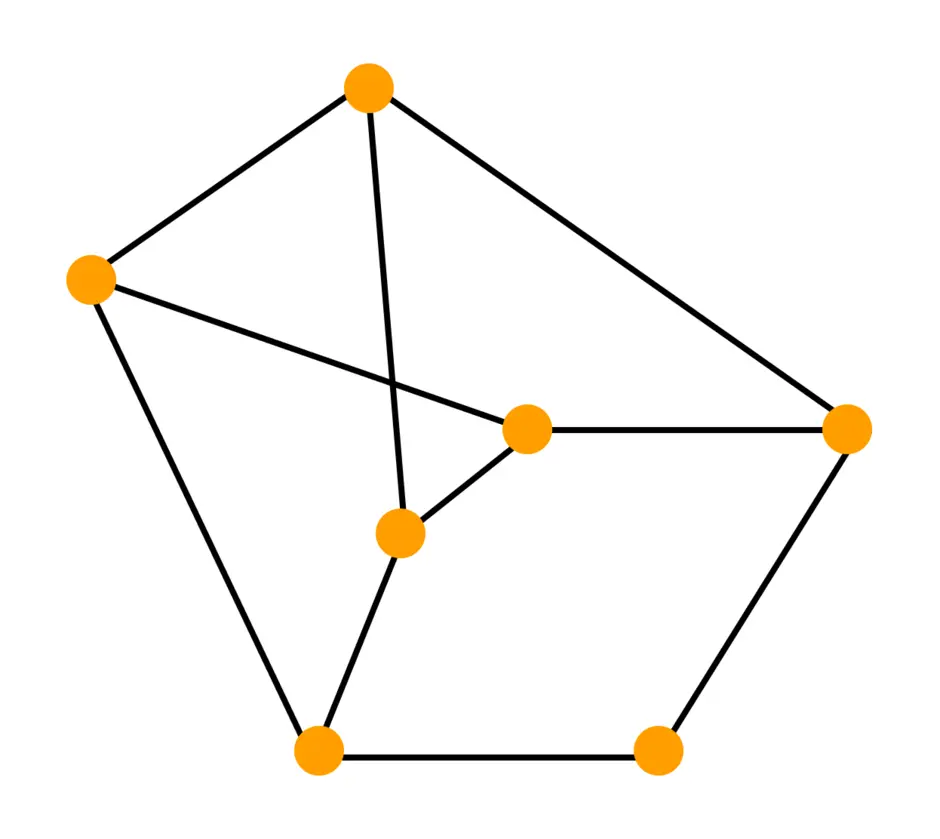
Один из методов обхода графа. Стратегия поиска в глубину, как и следует из названия, состоит в том, чтобы идти «вглубь» графа, насколько это возможно. Алгоритм поиска описывается рекурсивно: перебираем все исходящие из рассматриваемой вершины рёбра. Если ребро ведёт в вершину, которая не была рассмотрена ранее, то запускаем алгоритм от этой нерассмотренной вершины, а после возвращаемся и продолжаем перебирать рёбра. Возврат происходит в том случае, если в рассматриваемой вершине не осталось рёбер, которые ведут в нерассмотренную вершину. Если после завершения алгоритма не все вершины были рассмотрены, то необходимо запустить алгоритм от одной из нерассмотренных вершин.
Поделиться:
Поделиться:
Поделиться:
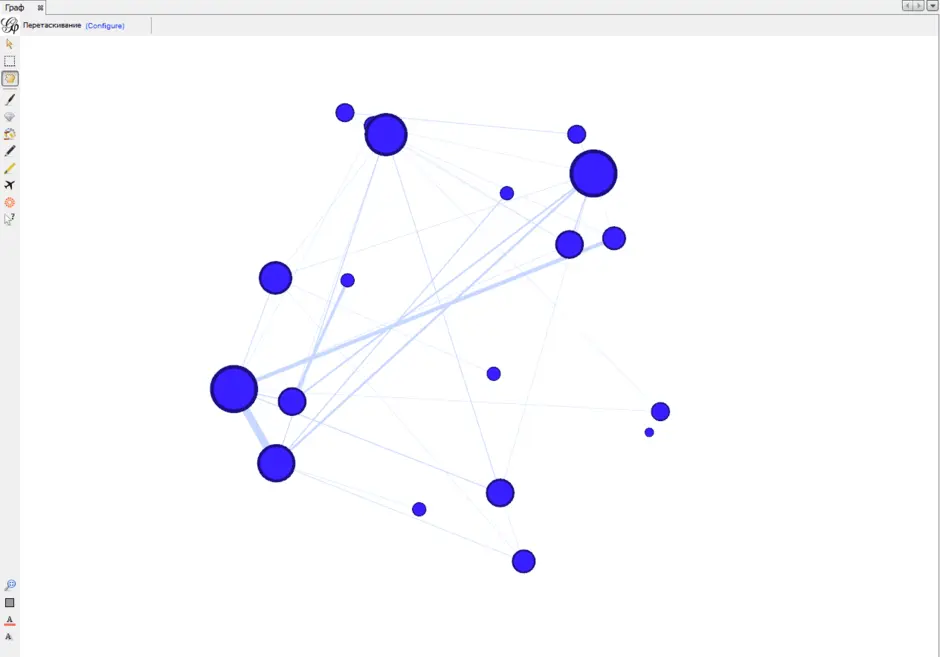
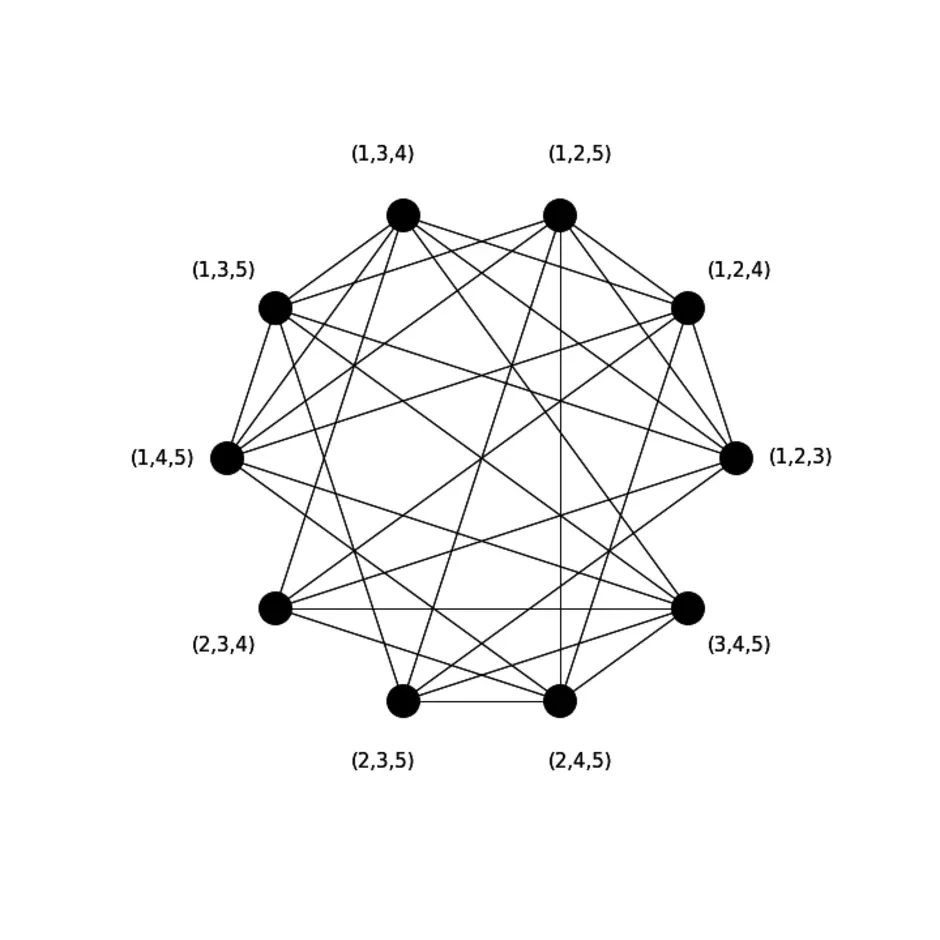
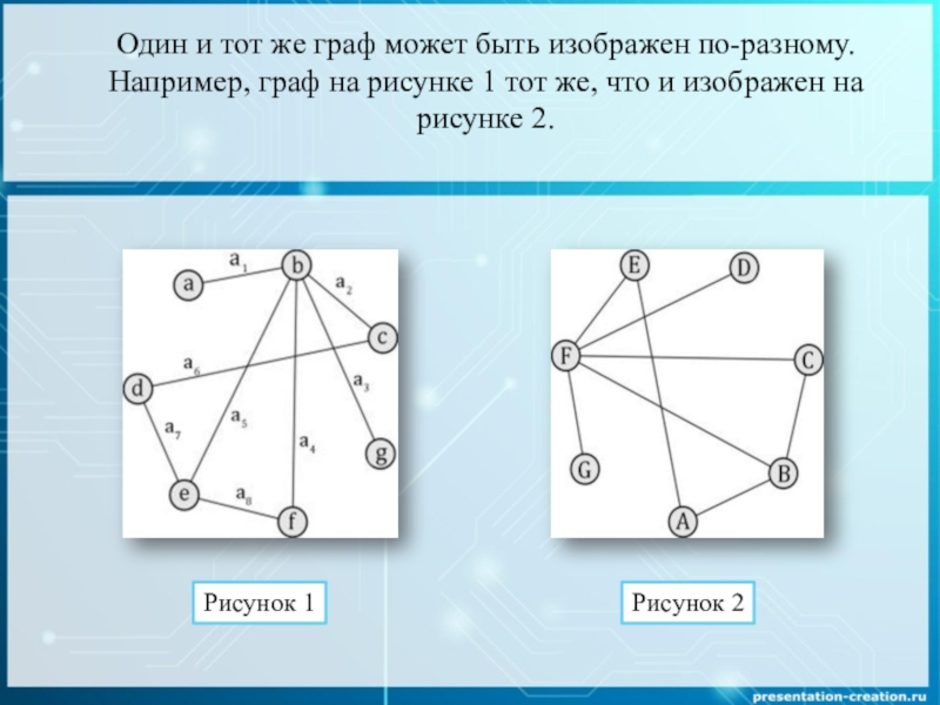
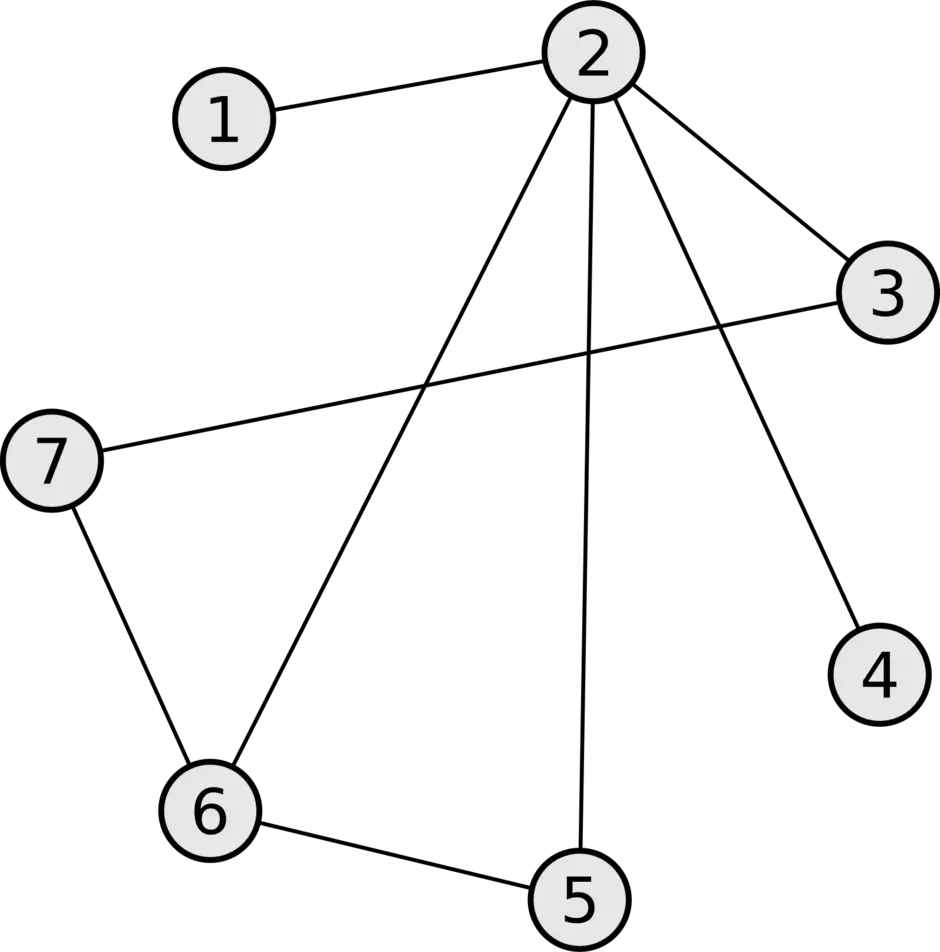
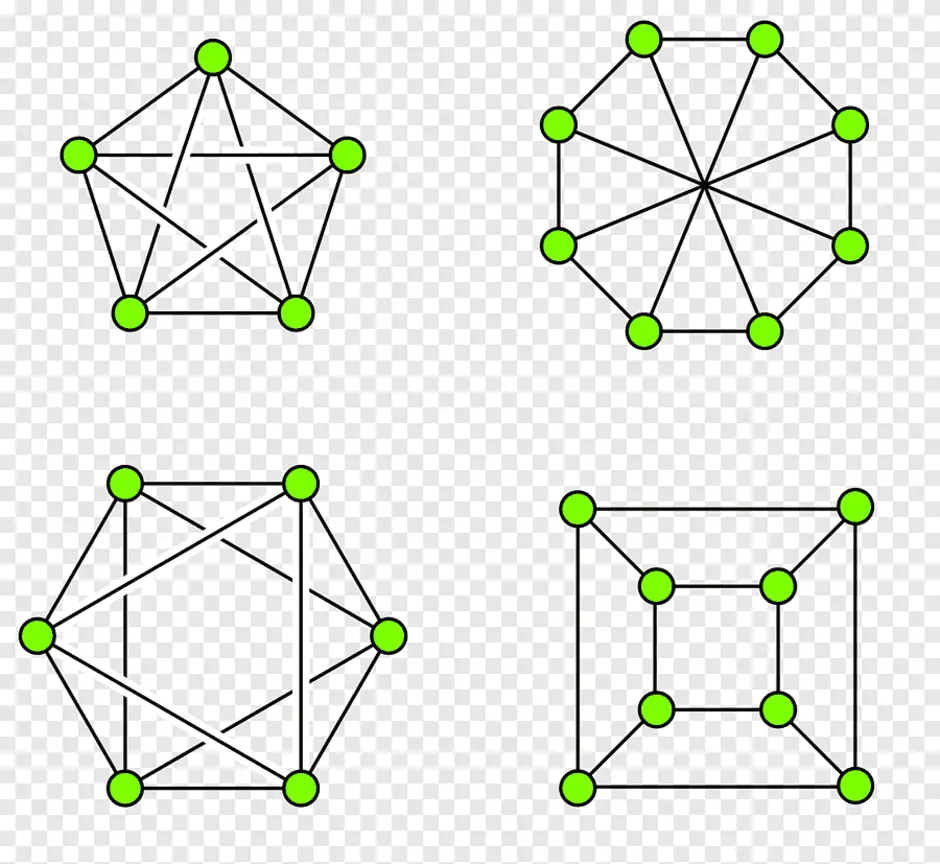
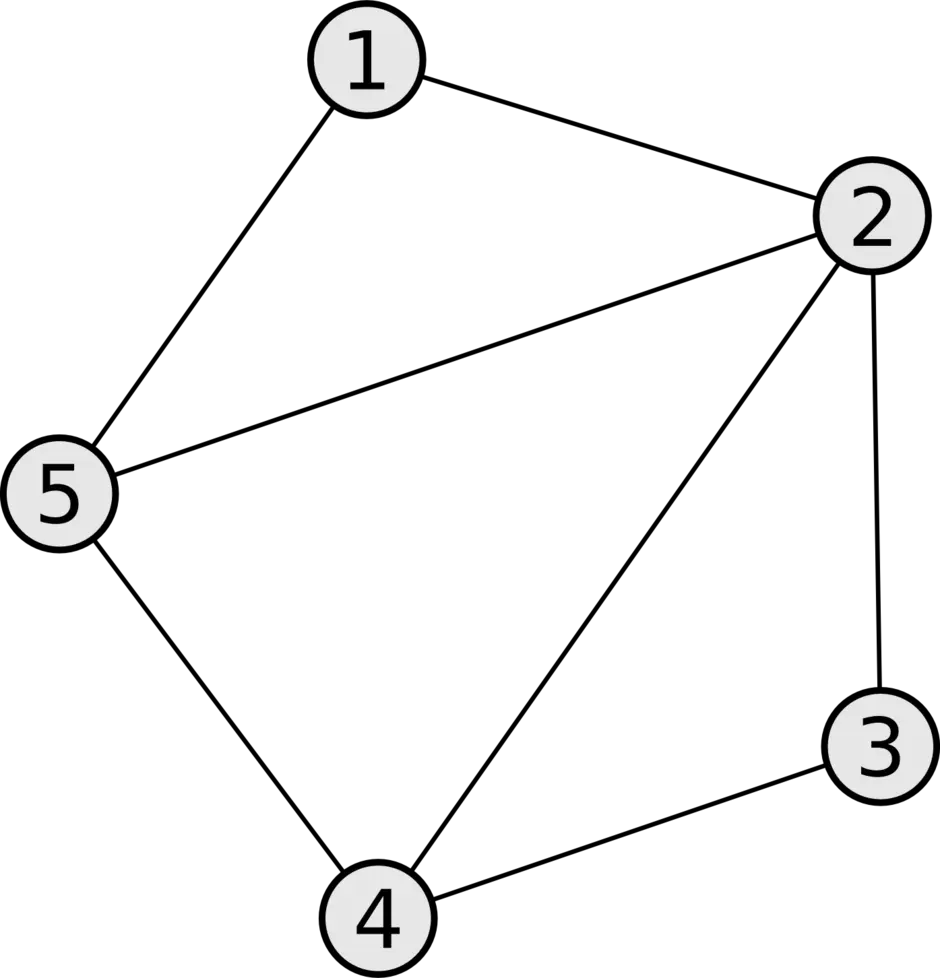
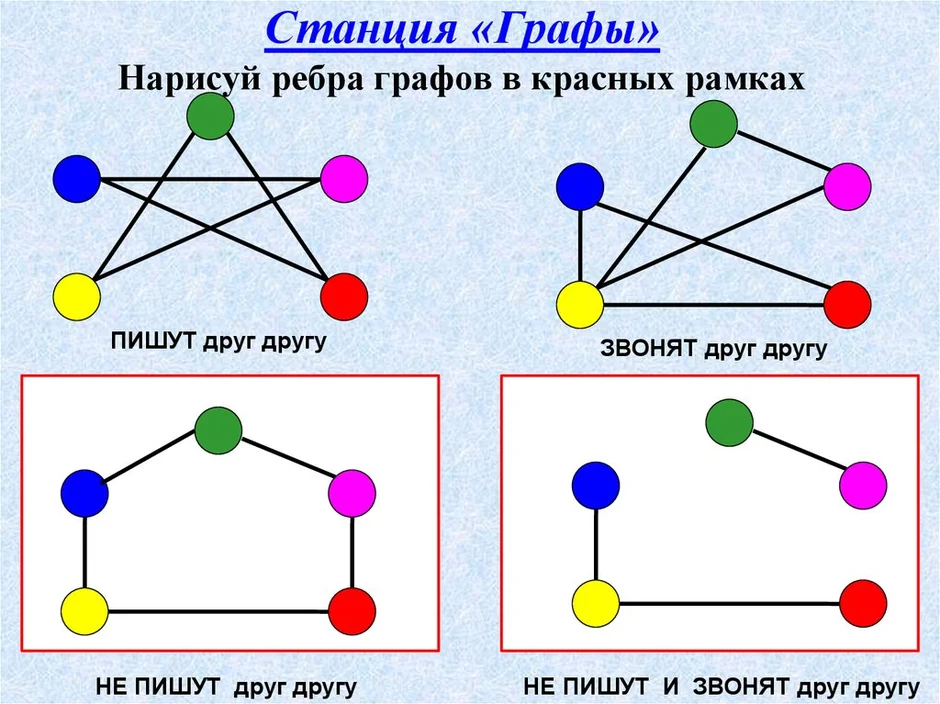
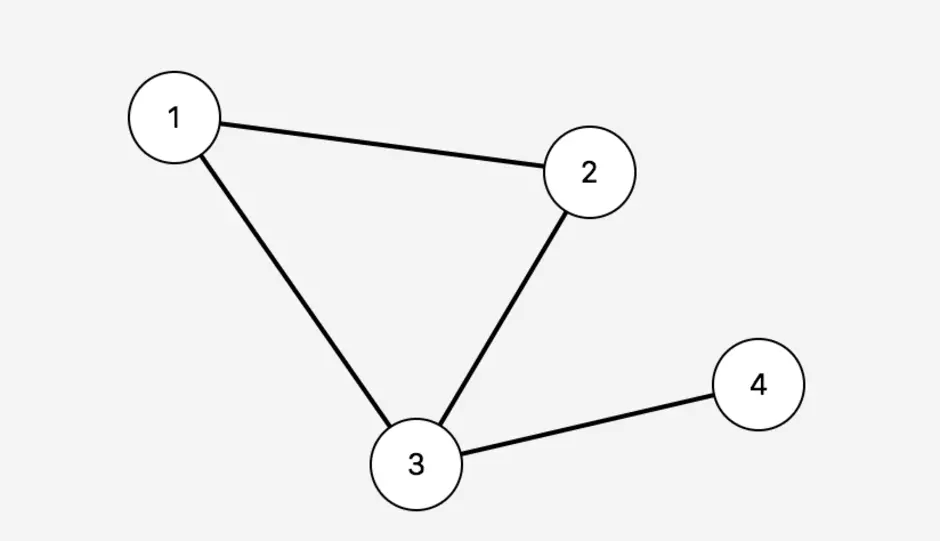
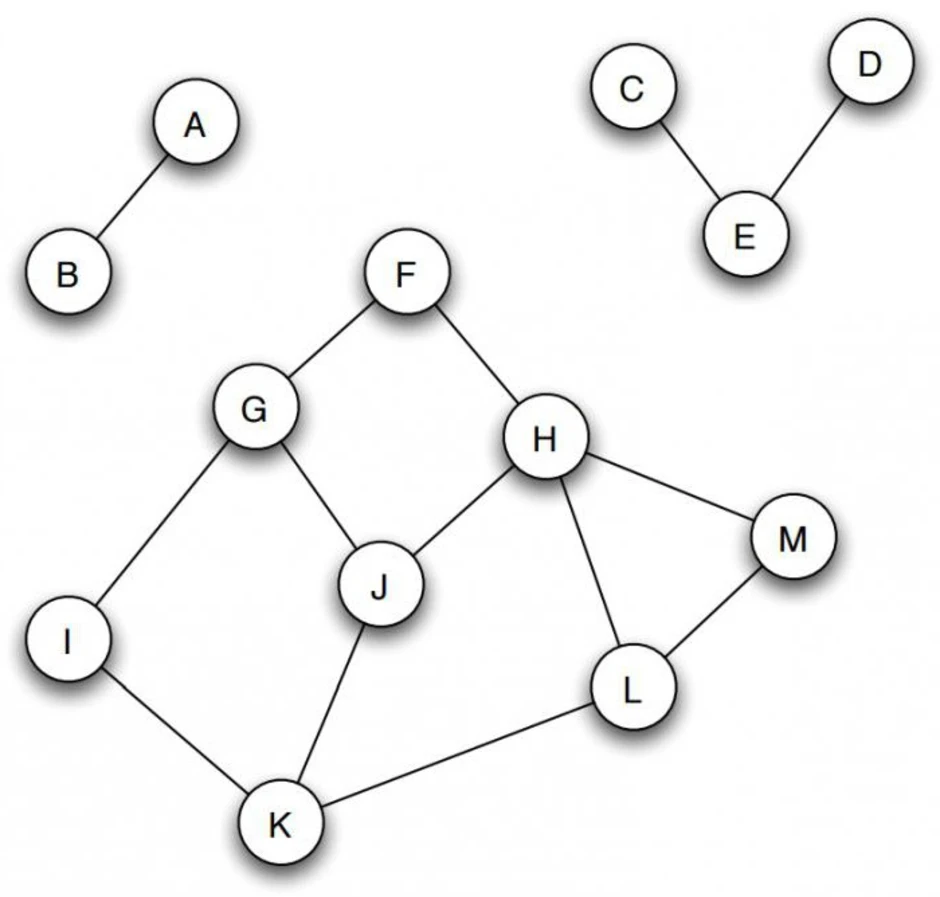
Раздел дискретной математики, изучающий графы. В самом общем смысле граф - это множество точек, которые соединяются множеством линий.
Поделиться:
Поделиться:
Поделиться:
Поделиться:
Поделиться:
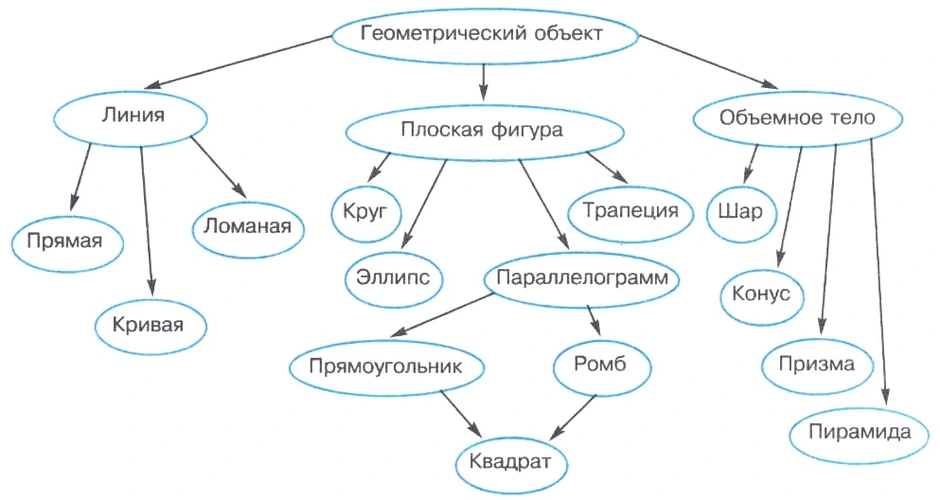
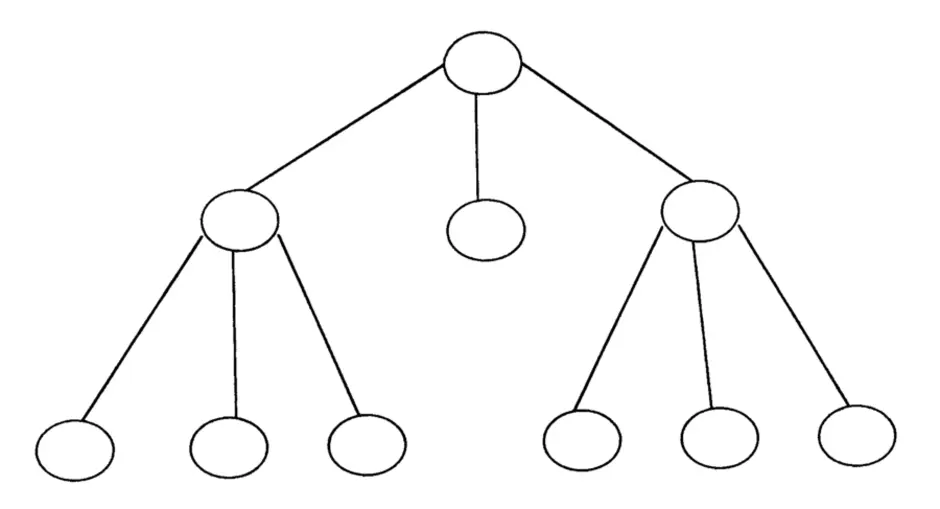
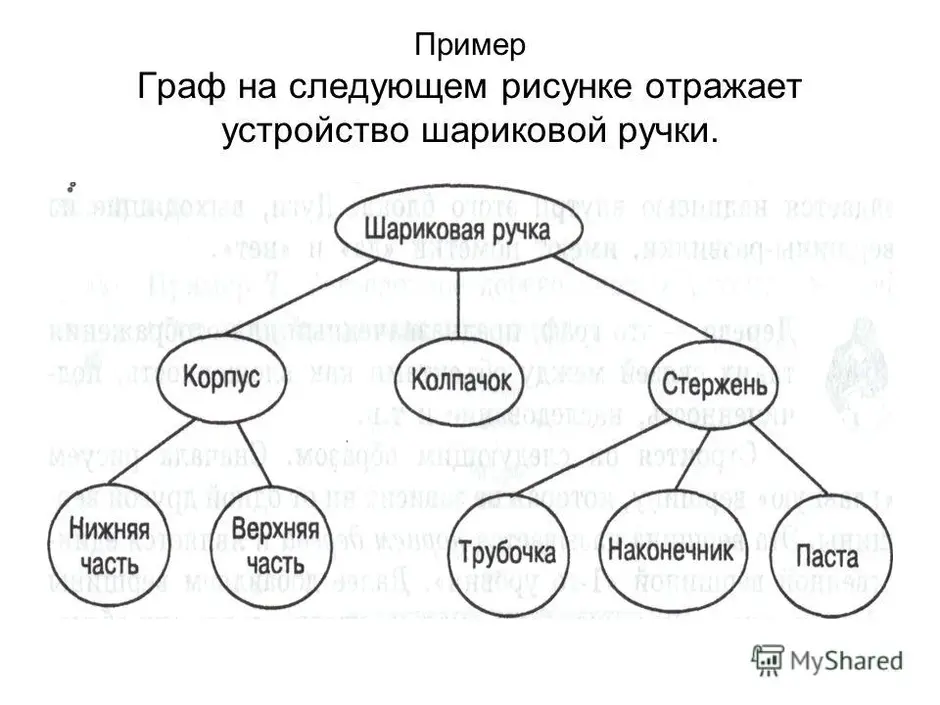
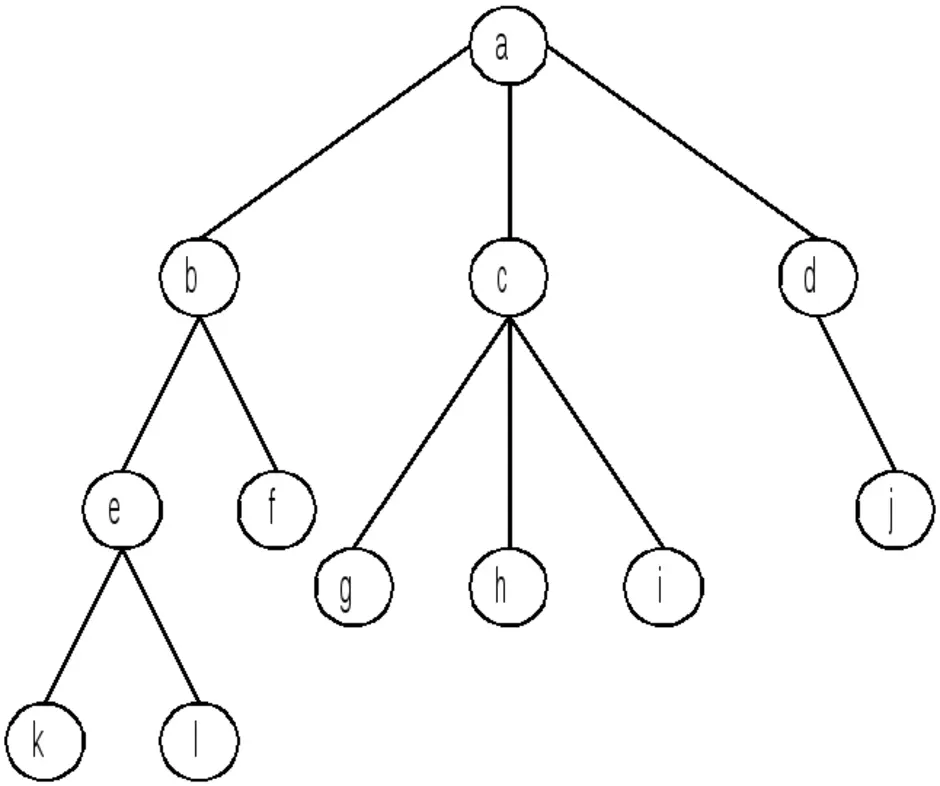
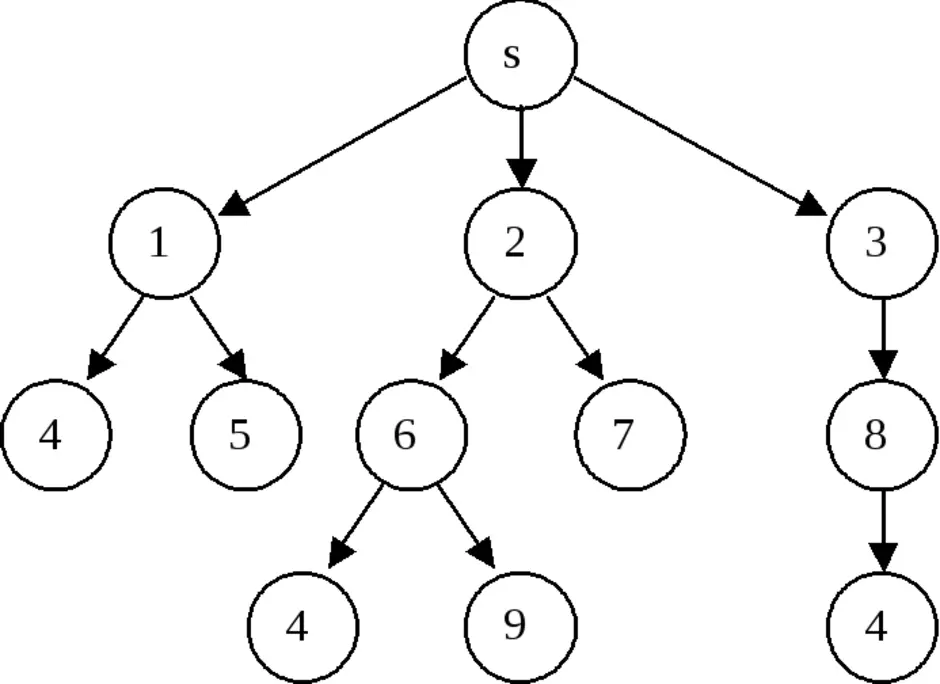
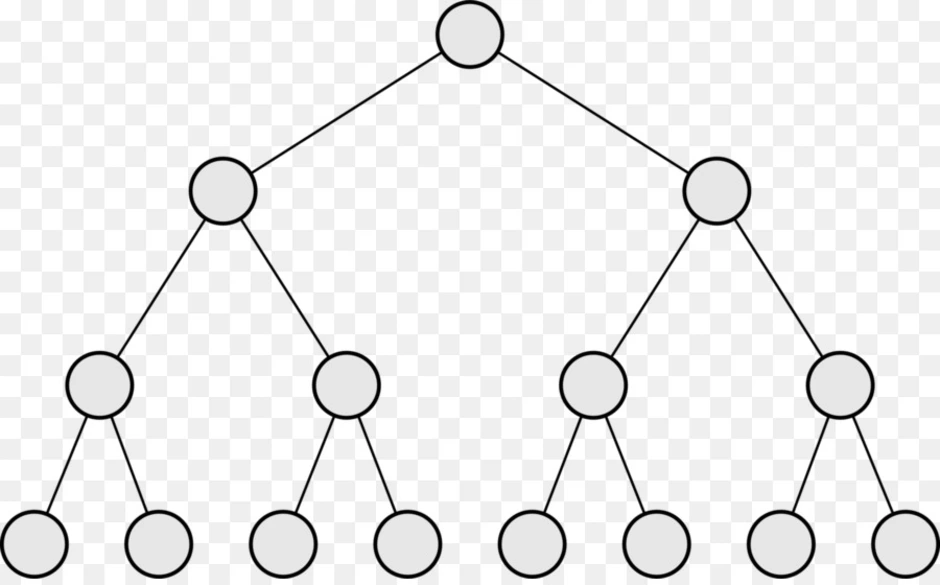
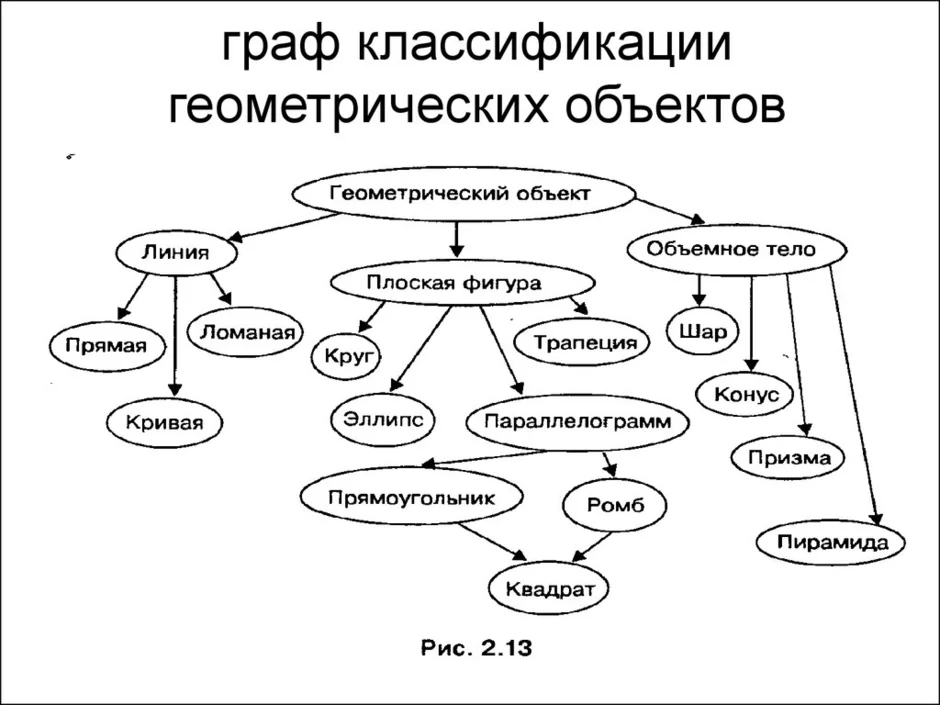
Это модель данных, где используется представление базы данных в виде древовидной структуры, состоящей из объектов различных уровней. Между объектами существуют связи, каждый объект может включать в себя несколько объектов более низкого уровня.
Поделиться:
Поделиться:
Поделиться:
Поделиться:
Поделиться:
Поделиться:
Поделиться:
Поделиться:
Поделиться:
Поделиться:
Поделиться:
Поделиться:
Поделиться:
Это связный ациклический граф. Связность означает наличие маршрута между любой парой вершин, ацикличность - отсутствие циклов. Отсюда, в частности, следует, что число рёбер в дереве на единицу меньше числа вершин, а между любыми парами вершин имеется один и только один путь.
Поделиться:
Поделиться:
Поделиться:

Поделиться:
Поделиться:
Поделиться:
Поделиться:
Поделиться:
Поделиться:
Поделиться: